top of page
Research interests

  • Acoustic wave ​propagation and simulation (in plate-like structures, shallow water, random media, pipes)

  • Sound source localization / acoustic imaging

  • Structural health monitoring

  • Uncertainty quantification and modeling

Projects
1. Passive Structural Health Monitoring of Aircraft 

We are developing passive structural health monitoring approaches using flow-induced ambient noise, including aircraft icing detection, damage imaging, bolt state identification, etc.

image.png

References:

  • Q. Qin, X. Wang*, J. He, and J. Lin, Passive reconstruction of dispersion curve in plates via flow-induced random vibration: The effect of boundary reflection and sensor placement, Ultrasonics, 137, 107178, 2024

  • Q. Qin, X. Wang*, Detecting ice on plate-like structures via flow-induced random vibration: A dispersion curve shift identification approach, to appear

​

2. Smart Urban Water Supply Systems - Pipeline defect detection

This project devotes to develop smart water pipeline systems that can monitor deficiency (leakage, blockage, burst, etc.) timely and efficiently.

Pipe system in the lab at HKUST

I have developed several transient wave-based inverse techniques for leakage detection. These techniques combine our pipeline transient wave model (altered for inverse problem solutions) with modern statistical inference methods. Initial theoretical, numerical and experimental results have been obtained, where one can refer to the publications below and download my codes for these algorithms from here. We are trying to apply our methodologies to more complex scenarios, for example, pipeline network, different pipe condition such as pipe wall material, real water supply systems with many uncertainties and unknown information.

​

References:

​

3. Acoustic source localization
3.1 Multi-source reconstruction with data and modeling uncertainties

This is my PhD work where I solved the problem of reconstructing multiple sound sources with data and modeling uncertainties. The uncertainties may originate from vibration of microphone array (for example in a moving car) or heat radiation (for example from a car engine), such that the microphone locations and wave propagation medium cannot be precisely known. This is a challenging problem, because one needs to quantify these uncertainties in a multi-parameter inverse problem which itself is difficult to solve. I proposed to quantify these uncertainties in the Dempster-Shafer framework (also known as belief functions or evidential theory) combining with Expectation-Maximization (EM) algorithm for simplifying the parameter dimension.

​

References:

​

3.2 Sound source localization in complex media

We solve sound source localization problems in different complicated scenarios, such as random medium and ocean (shallow water). This needs a profound physical understanding and numerical simulation of the acoustic wave propagation in the considered scenario, as well as appropriate inverse methods for each specific problem (such as beamforming, time reversal, and our newly proposed methods).​

​

Random medium
Forward problem:
Wave propagation simulation using Spectral-Element Method
Inverse problem:
Sound source localization using Time Reversal

References:

Ocean (shallow water)
Sound propagation simulation in shallow water using SPEFEM2D (Spectral-Element Method)

References:

4. Uncertainty quantification

Uncertainty quantification (UQ) is the quantification of uncertainties in Quantity of Interest (QoI) propagated from uncertain inputs. It focuses on the influence on the QoI from the parametric variability listed in the sources of uncertainty. We have proposed a full UQ scheme to compute the distribution and sensitivity of QoI using advanced sampling and modeling methods. The methodologies have been applied in engineering problems, such as underwater sound source localization and droplet evaporation.

​

References:

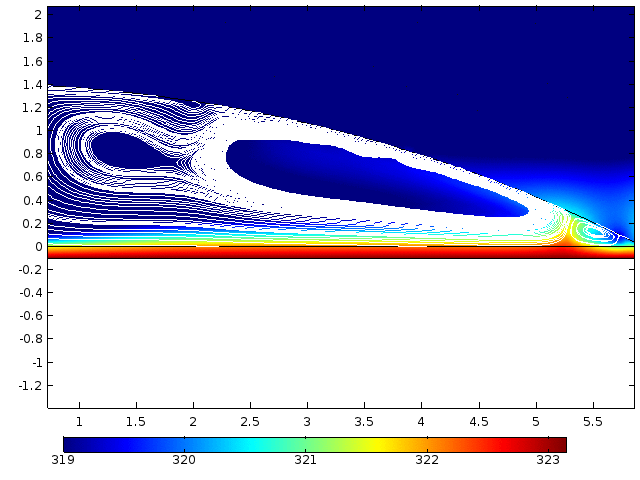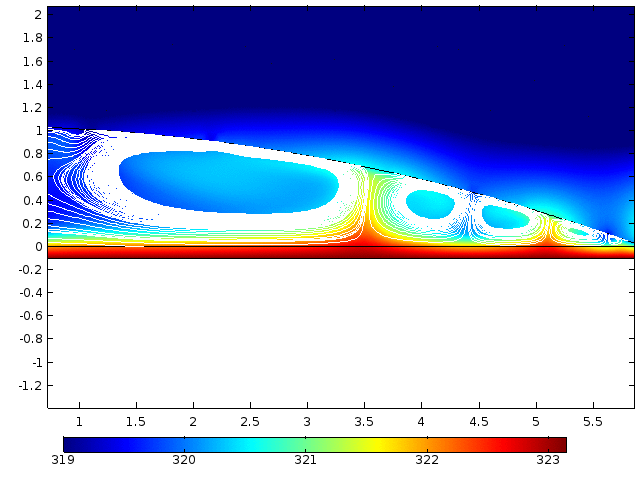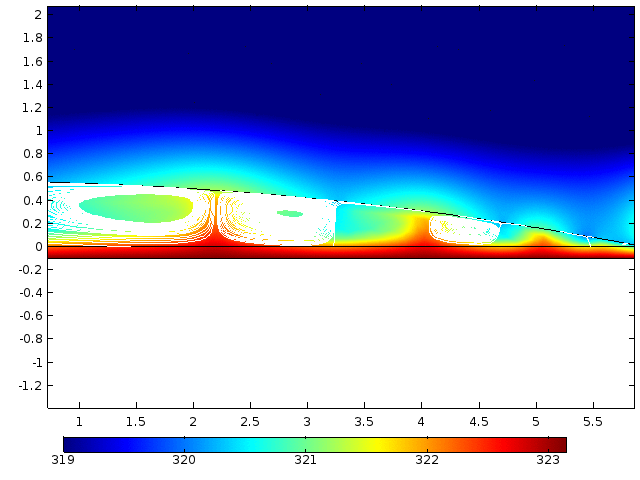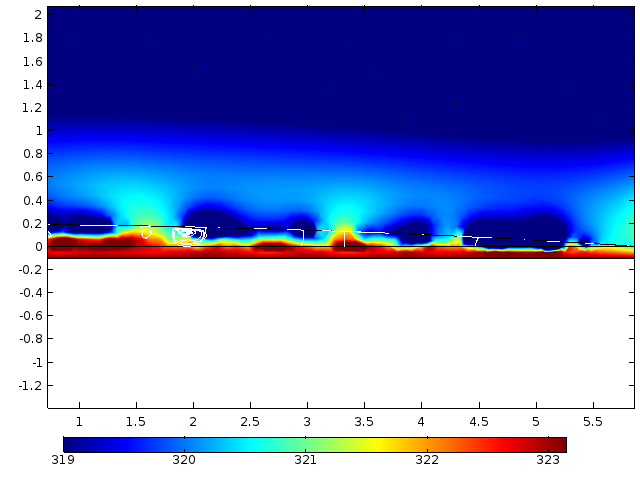
Numerical simulation of droplet evaporation
Response surface of droplet flow pattern with uncertain parameters obtained via Kriging
5. Set-valued and interval-valued statistics

In many practical problems, the data cannot be precisely measured, but a possible range (a set or an interval) is given. In some other cases, the data themselves are set-valued or interval-valued, for example daily temperature and daily stock price. We generalize basic concepts in classical probability theory (e.g., variance and covariance) to the set-valued and interval-valued cases. We also generalize classical statistical models (linear model and time series models) and study their mathematical and statistical properties.

​

References:

Interval-valued time series that describes daily stock price
bottom of page